Back

The quantum Hall effect has been a rich source of novel quantum phenomena over its thirty-four-year history: the combination of topological order and strongly correlated non-Fermi liquid behavior gives rise to dissipationless edge currents, fractionalized statistics and a slew of other interesting features. However, realizing the fractional quantum Hall effect (FQHE) in the conventional setting of a high-mobility semiconductor heterostructure in a high magnetic field remains experimentally difficult. In recent years, the field has seen a surge of interest from proposals for realizing FQH phenomena in lattice systems, without the need for a large external field: so-called fractional Chern insulators (FCIs) [1-2]. These states have the potential to be stable at room temperature, and there are many possible routes to realise them experimentally. FCIs also raise theoretical questions independent of their experimental interest: notably, FCI phenomena constitute a non-trivial and poorly-understood generalization of the FQHE in which lattice effects are significant.

Our group has taken some important steps towards the development of a unified theoretical treatment of FQH-FCI phenomena, with our work falling into two broad categories. In the first strand, we have identified band geometric features (including the Berry curvature and quantum metric) as important factors in determining the suitability of a lattice model for realising FQH physics [3–5]. In the second strand, we have applied these ideas, and others, to the study of specific FCI models, with a particular focus on the Hofstadter model [6–7].

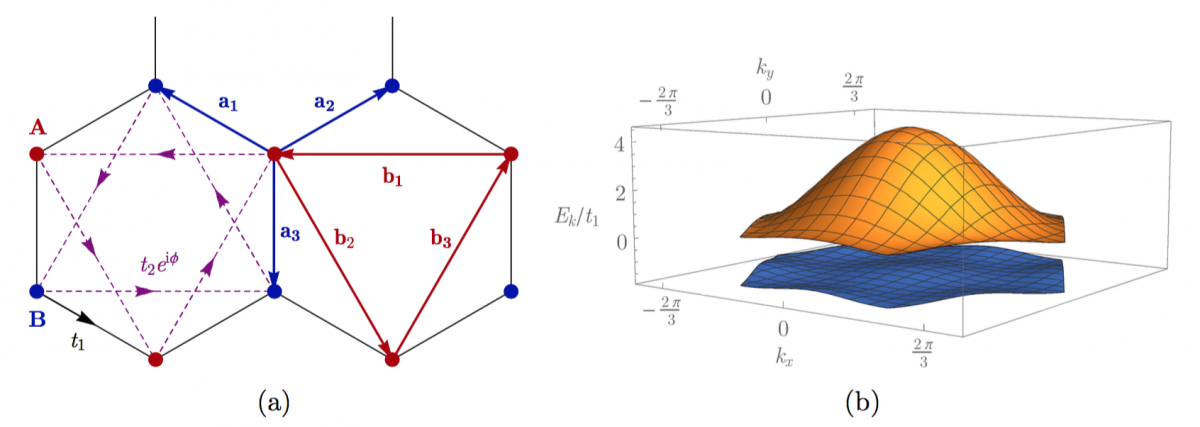
Figure: (a) The Haldane honeycomb (HH) model [25], an example of an FCI. (b) The band structure of the HH model, with parameters chosen to generate an extremely flat lowest band.

References

[1]     S. A. Parameswaran, R. Roy, and S. L. Sondhi, C. R. Phys. 14, 816 (2013).
[2]     E. J. Bergholtz and Z. Liu, Int. J. Mod. Phys. B 27, 1330017 (2013).
[3]     S. A. Parameswaran, R. Roy, and S. L. Sondhi, Phys. Rev. B 85, 241308 (2012).
[4]     R. Roy, Phys. Rev. B 90, 165139 (2014).
[5]     T. S. Jackson, G. Moller, and R. Roy, Nat. Commun. 6, 8629 (2015).
[6]     F. Harper, S. H. Simon, and R. Roy, Phys. Rev. B 90, 075104 (2014).
[7]     D. Bauer, T. S. Jackson, and R. Roy, Phys. Rev. B 93, 235133 (2016).
[25]    F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).