Back

Inspired by previous work on the W∞ algebra, our group further investigated the suitability of lattice models to support fractional Chern insulator states. Given a family of normalised vectors, in this case the Bloch wavefunctions, a natural way of defining a distance measure [30] is the following:

\[ \mathrm{d}l^2 =g_{ij}\mathrm{d}k_i\mathrm{d}k_j=\left(\mathrm{d}\psi,\mathrm{d}\psi\right)-\left|\left(\psi,\mathrm{d}\psi\right)\right|^2\\ \mathrm{d}\psi(k)=\psi\left(k+\mathrm{d}k\right)-\psi(k). \]

We found that this quantum metric plays an important role in the stability of lattice models. Rather surprisingly (see figure), we discovered that a complete isomorphism of algebras between the FQH and FCI cases can be obtained if only three conditions are satisfied. These conditions are that the Berry curvature B(k) and quantum metric defined above should be constant over the Brillouin zone. The third condition is that 

\[ D(k)=\mathrm{det}g(k)-\frac{\left[B(k)\right]^2}{4}=0. \]

In Ref. [4] we showed that D(k) is always nonnegative, and that the resulting metric determinant inequality D(k) ≥ 0 measures deviations from lowest Landau level physics, specifically, unlike the first two conditions. When these three conditions are met, that the commutator of two projected density operators has a modified GMP form. Since it impossible to obtain perfectly uniform Berry curvature in models with local hopping and a finite number of bands, we conjectured that a deviation of D(k) away from zero should act to destabilize FCI states on a given lattice model. We also proved the related identity 

\[ T(k)=\mathrm{tr}g(k)-\left|B(k)\right|\geq 0, \]

and showed that T(k) = 0 implies D(k) = 0. This identity, which doesn't seem to have been noticed before, connects the two most important quantum geometric features, the Berry curvature and the quantum metric. The vanishing of the metric trace inequality corresponds to the stronger condition that the algebra of band-projected density operators is identical to the LLL GMP algebra, rather than just isomorphic to it.

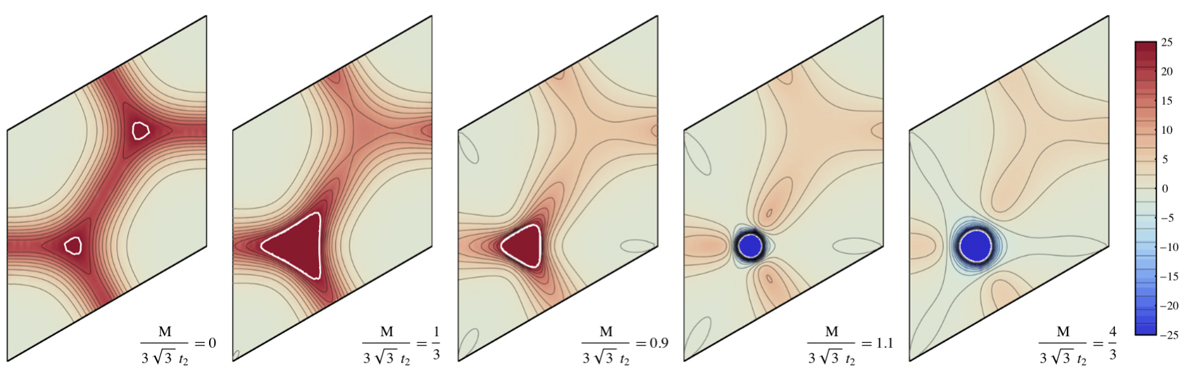
Figure 1: Contour plots of the distribution of Berry curvature over a unit cell of the reciprocal lattice for the Haldane honeycomb model [23]; this unit cell was chosen so as to not split up the Brillouin-zone corners, which appear to be points of high Berry curvature. The same color scale is used in each panel.

 

References

[4]     R. Roy, Phys. Rev. B 90, 165139 (2014).
[30]    J. P. Provost and G. Vallee, Comm. in Math. Phys. 76, 289–301 (1980).