FQHE and Fractional Chern Insulators
Click here to expand all sections.
Overview of Fractional Chern Insulators
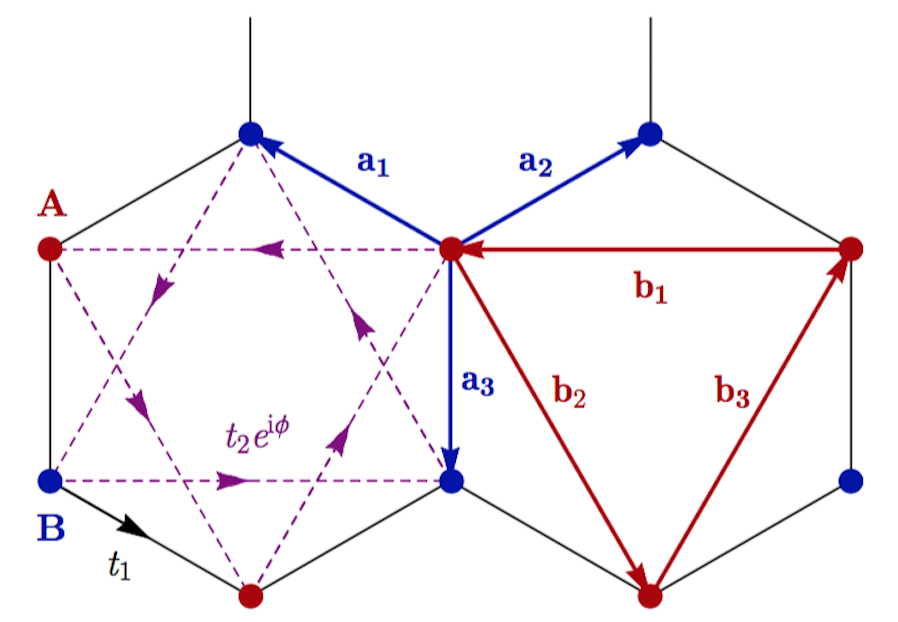
an example of an FCI.
The quantum Hall effect has been a rich source of novel quantum phenomena over its thirty-four-year history: the combination of topological order and strongly correlated non-Fermi liquid behavior gives rise to dissipationless edge currents, fractionalized statistics and a slew of other interesting features. However, realizing the fractional quantum Hall effect (FQHE) in the conventional setting of a high-mobility semiconductor heterostructure in a high magnetic field remains experimentally difficult. In recent years, the field has seen a surge of interest from proposals for realizing FQH phenomena in lattice systems, without the need for a large external field: so-called fractional Chern insulators (FCIs) [1-2]. These states have the potential to be stable at room temperature, and there are many possible routes to realise them experimentally. FCIs also raise theoretical questions independent of their experimental interest: notably, FCI phenomena constitute a non-trivial and poorly-understood generalization of the FQHE in which lattice effects are significant.
Band Geometry
Fractional Chern Insulators and the W∞ algebra
The basic theoretical puzzle posed by FCIs is to provide a microscopic description of their physics. A number of theoretical works have attempted to bridge the gap between FCIs and FQHE including adiabatic continuity of Wannier functions [8–9], the extended Hamiltonian formalism [10], parton/slave particle treatments [11] and attempts to characterize interactions using pseudopotentials [12–13], among others. While these approaches provide a number of useful insights into the problem, they generically don’t distinguish between different single-particle flat band Hamiltonians; however, numerical work [14–15] has found that single-particle effects can strongly influence the stability of FCI phases. In an effort to better understand these single-particle effects, our group has taken several important steps towards the development of a unified theoretical treatment of FQH-FCI phenomena.
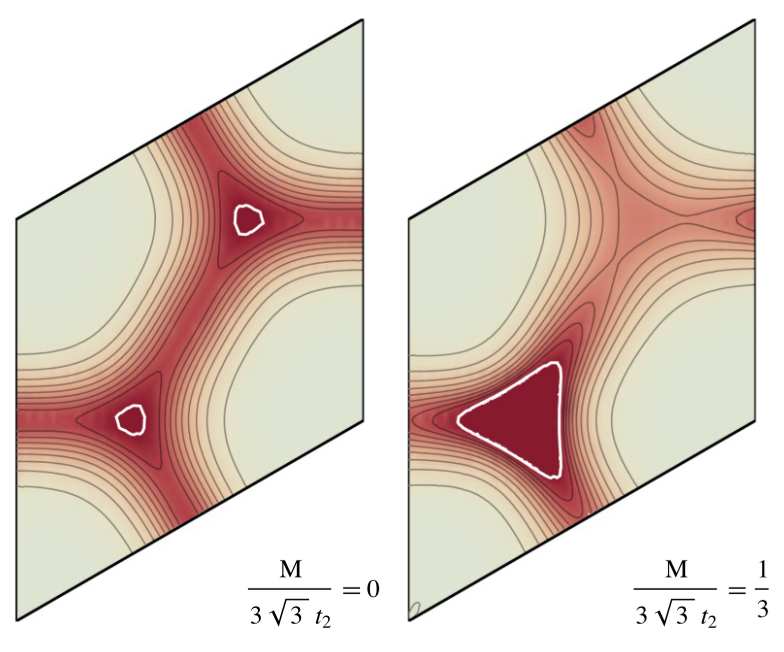
for a particular FCI model.
Band geometry of fractional topological insulators
Inspired by previous work on the W∞ algebra, our group further investigated the suitability of lattice models to support fractional Chern insulator states. Rather surprisingly (see figure), we discovered that a complete isomorphism of algebras between the FQH and FCI cases can be obtained if only three conditions are satisfied. Briefly stated, these conditions are that the Berry curvature B(k) and pull-back of the Hilbert space metric g(k) (referred to as the “quantum metric”) should be constant over the Brillouin zone. The third condition relates the determinant of g(k) to the Berry curvature.
Geometric stability of topological lattice phases
The theoretical work in Refs [3–4] led us to propose a “geometric stability hypothesis,” which states that an approximate version of the single-mode approximation remains valid in FCI models, and that curvature and metric fluctuations along with the trace inequality are the relevant parameters measuring the deviation of a single-particle lattice Hamiltonian from Landau level physics. In Ref. [5] we conducted extensive numerical simulations on a scale beyond anything carried out in previous literature, comprehensively sampling the parameter space at thousands of values for three of the best-studied FCI models. Using a two-step sampling procedure, we were able to distinguish the effects caused by fluctuations of the Berry curvature and Hilbert space metric; the manuscript is the first work to demonstrate the importance of the latter factor.
Model Systems
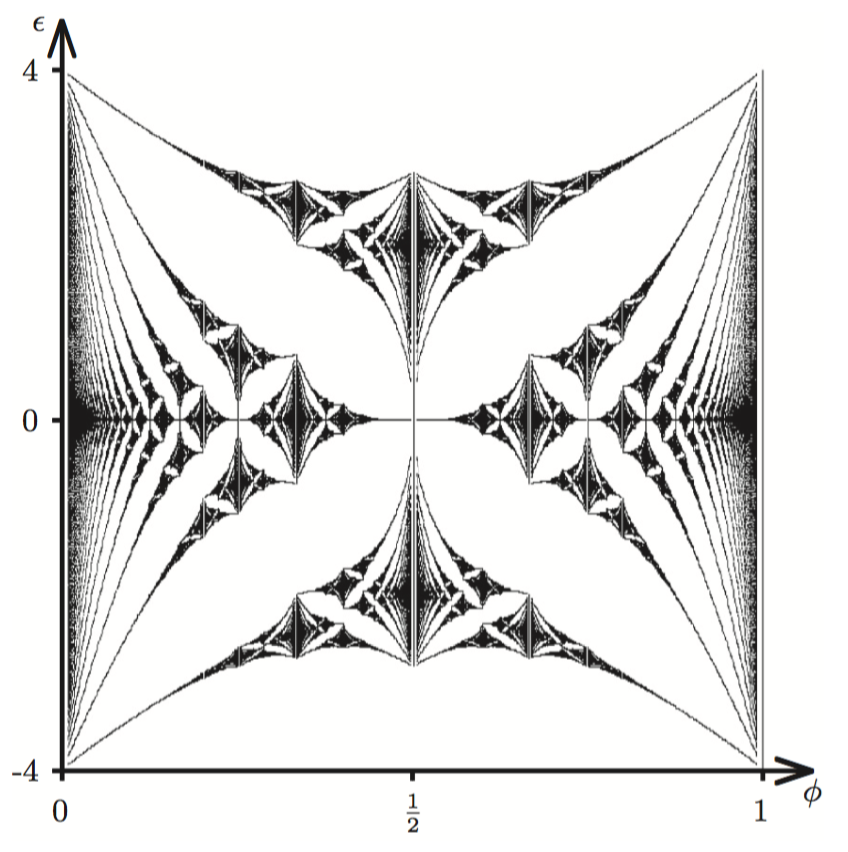
Perturbative Approach to Flat Chern Bands in the Hofstadter Model
The Hofstadter model [17–18] describes a charged particle hopping on a lattice in the presence of a magnetic field, and is noted for its fractal energy spectrum. Recently, the model has generated renewed interest as a system that bridges the gap between the continuum quantum Hall effects and lattice-based Chern insulators. In Ref. [6] we pursue this connection in detail at the single- and many-body level. In the process, we draw connections to recent experimental realisations of the Hofstadter model [19–20] and, significantly, make analytical progress in a field that has mostly been the subject of numerical studies. The method we present is a general approach that can be applied to a variety of interactions, lattices and parameter ranges.
Quantum geometry and stability of the fractional quantum Hall effect in the Hofstadter model
The perturbative study of Ref. [6] suggested that the Hofstadter model would provide an exciting setting for studying the relationship between geometry and FQHE physics in a controlled fashion. Motivated by the geometric stability hypothesis [5], in Ref. [7], we further studied the geometry of the Hofstadter bands in the small flux per plaquette limit. We found that, as with the dispersion and Berry curvature, fluctuations in the quantum metric are exponentially suppressed as the magnetic flux decreases. In contrast, the deviation from saturation of the geometric inequalities falls off polynomially. This suggests that these inequalities are the dominant measure of closure of the density operator algebra near the continuum limit.
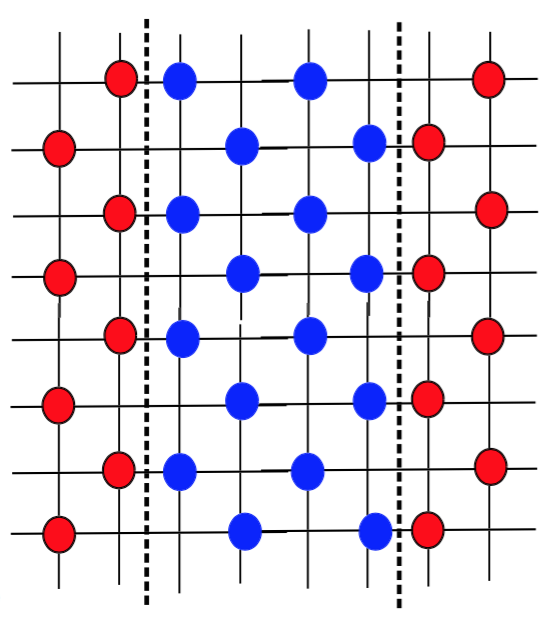
Generalizing quantum Hall ferromagnetism to fractional Chern bands
In multicomponent QH systems at integer fillings, ground states that have topological order and also spontaneously break symmetries can arise, a phenomenon termed QH ferromagnetism (QHFM) [26,27]. An important feature of such states is that the broken symmetry can persist to nonzero temperatures, even as quantum Hall order is lost, as in the celebrated case of bilayer systems at filling factor ν = 1 [28]. In Ref. [29], we studied the interplay between quantum Hall ordering and spontaneous sublattice symmetry breaking in multiple-Chern-number bands at fractional fillings.
References
[1] S. A. Parameswaran, R. Roy, and S. L. Sondhi, C. R. Phys. 14, 816 (2013).
[2] E. J. Bergholtz and Z. Liu, Int. J. Mod. Phys. B 27, 1330017 (2013).
[3] S. A. Parameswaran, R. Roy, and S. L. Sondhi, Phys. Rev. B 85, 241308 (2012).
[4] R. Roy, Phys. Rev. B 90, 165139 (2014).
[5] T. S. Jackson, G. Moller, and R. Roy, Nat. Commun. 6, 8629 (2015).
[6] F. Harper, S. H. Simon, and R. Roy, Phys. Rev. B 90, 075104 (2014).
[7] D. Bauer, T. S. Jackson, and R. Roy, Phys. Rev. B 93, 235133 (2016).
[8] X.-L. Qi, Phys. Rev. Lett. 107, 126803 (2011).
[9] Y.-L. Wu, N. Regnault, and B. A. Bernevig, Phys. Rev. B 86, 085129 (2012).
[10] G. Murthy and R. Shankar, Phys. Rev. B 86, 195146 (2012).
[11] J. McGreevy, B. Swingle, and K.-A. Tran, Phys. Rev. B 85, 125105 (2012).
[12] C. H. Lee, R. Thomale, and X.-L. Qi, Phys. Rev. B 88, 035101 (2013).
[13] Y.-L. Wu, N. Regnault, and B. A. Bernevig, Phys. Rev. Lett. 110, 106802 (2013).
[14] D. N. Sheng, Z.-C. Gu, K. Sun, and L. Sheng, Nat. Commun. 2, 389 (2011).
[15] Y.-L. Wu, B. A. Bernevig, and N. Regnault, Phys. Rev. B 85, 075116 (2012).
[16] S. Girvin, A. H. MacDonald, and P. Platzman, Phys. Rev. B 33, 2481 (1986).
[17] D. Hofstadter, Phys. Rev. B 14, 2239 (1976).
[18] P. G. Harper, P. R. Soc. A 68, 879 (1955).
[19] H. Miyake, G. A. Siviloglou, C. J. Kennedy, W. C. Burton, and W. Ketterle, Phys. Rev. Lett. 111, 185302 (2013).
[20] M. Aidelsburger, M. Atala, M. Lohse, J. T. Barreiro, B. Paredes, and I. Bloch, Phys. Rev. Lett. 111, 185301 (2013).
[21] F. D. M. Haldane, Phys. Rev. Lett. 51, 605 (1983).
[22] B. I. Halperin, Helv. Phys. Acta 56, 75 (1983).
[23] F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).
[24] X. Hu, M. Kargarian, and G. A. Fiete, Phys. Rev. B 84, 155116 (2011).
[25] F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).
[26] S. L. Sondhi, A. Karlhede, S. A. Kivelson, and E. H. Rezayi, Phys. Rev. B. 47, 16419 (1993).
[27] T. Jungwirth and A. H. MacDonald, Phys. Rev. B. 63, 035305 (2000).
[28] A. R. Champagne, J. P. Eisenstein, L. N. Pfeiffer, and K. W. West, Phys. Rev. Lett. 100, 096801 (2008).
[29] A. Kumar, R. Roy, and S. L Sondhi, Phys. Rev. B 90, 245106 (2014).
[30] J. P. Provost and G. Vallee, Comm. in Math. Phys. 76, 289–301 (1980).