Earlier Work
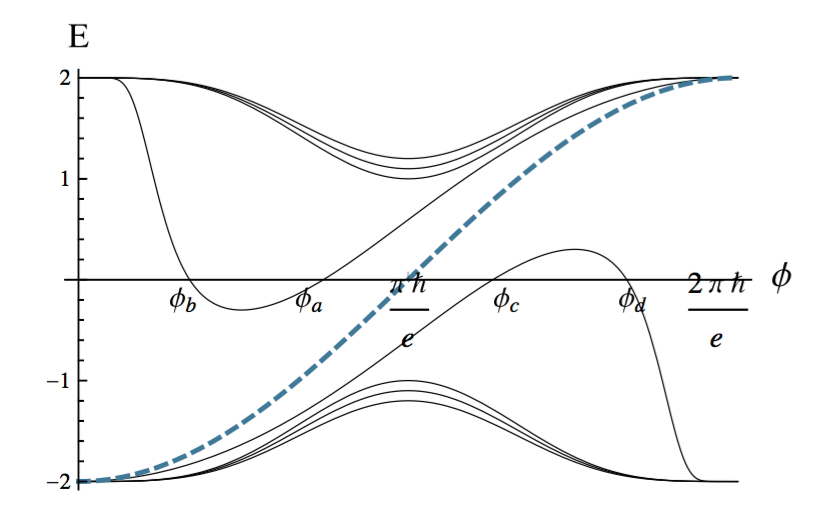
flux for a model superconductor
Topological Majorana and Dirac Zero Modes in Superconducting Vortex Cores
In Ref. [1], we provided an argument based on flux insertion to show that certain superconductors with a nontrivial topological invariant have protected zero modes in their vortex cores. This argument has the flavor of a two-dimensional index theorem and applies to disordered systems as well. It also provides a new way of understanding the zero modes in the vortex cores of a spinless px + ipy superconductor. Applying this approach to superconductors with and without time-reversal and spin-rotational symmetry, we predicted the necessary and sufficient conditions for protected zero modes to exist in their vortices.
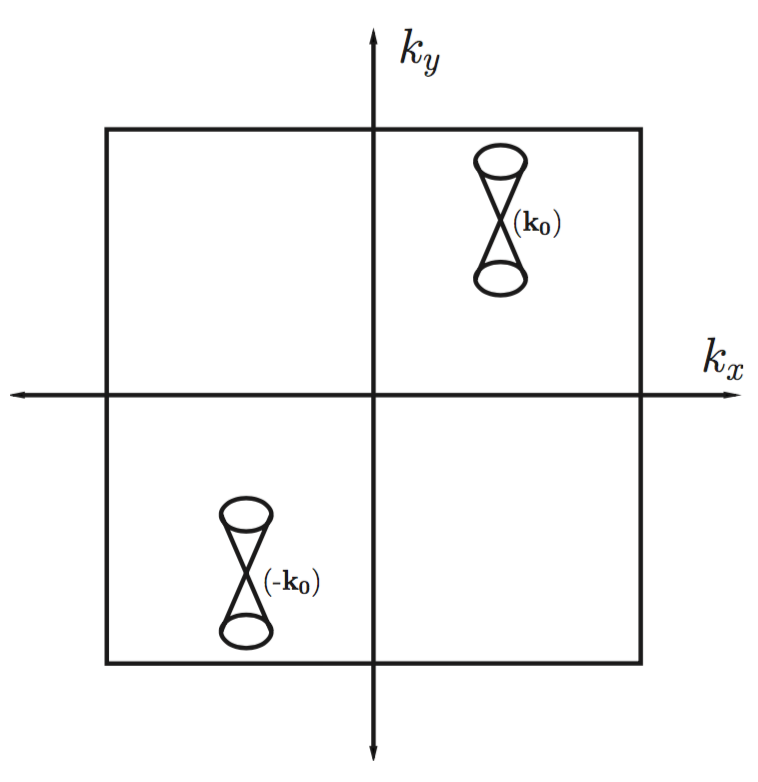
spectrum of a Hamiltonian
Topological phases and the quantum spin Hall effect in three dimensions
In Ref. [2], we showed the existence of topological phases of Bloch insulators with time-reversal symmetry in three dimensions. These phases are characterized by topological Z2 invariants whose stability is studied using band-touching arguments. Unlike insulators which break time-reveral symmetry, some of these topological phases are intrinsically three dimensional. The number of invariants (four) needed to specify the phase of these insulators also differs from the time-reversal-breaking case. We also investigated the relation between these phases and the quantum spin Hall effect in three dimensions.
Z2 classification of quantum spin Hall systems: An approach using time-reversal invariance
In Ref. [3], we studied the phases of Bloch insulators with time-reversal symmetry on the basis of the homotopy of the ground-state wave functions in momentum space and found that there are two topological classes characterized by a Z2 invariant. The results were in agreement with the study in Ref. [4] based on counting the zeroes of a certain Pfaffian function related to the ground-state wave function. We showed that there is a link between the formulation of the topological invariant and the number of robust edge states. A formula was also provided which greatly simplifies the computation of the invariant in a large number of cases. The study provided guidance for the search of systems which belong to the nontrivial topological class and also established a link between the quantum spin Hall effect and the integer quantum Hall effect.
Collective modes and electromagnetic response of a chiral superconductor
Motivated by the controversy surrounding the Kerr effect measurements in strontium ruthenate [5], in Ref. [6] we examined the electromagnetic response of a clean chiral p-wave superconductor. When the contributions of the collective modes are accounted for, we found that the Hall response in a clean chiral superconductor is smaller by several orders of magnitude than previous theoretical predictions, and is too small to explain the experiment. We also uncovered some unusual features of the collective modes of a chiral superconductor, namely, that they are not purely longitudinal and couple to external transverse fields.
Topological superfluids with time reversal symmetry
In Ref. [7] we showed that superfluids in two and three dimensions which have time reversal invariant ground states have phases which are distinguished by a topological invariant. We showed further that the B-phase of 3He is a superfluid in the non-trivial topological class. Superfluids in the non-trivial topological class are shown to have gapless edge states and support various kinds of vortices with zero energy modes localized in their cores. Some of these vortices have non-Abelian statistics.
References
[1] R. Roy, Phys. Rev. Lett. 105, 186401 (2010).
[2] R. Roy, Phys. Rev. B 79, 195322 (2009).
[3] R. Roy, Phys. Rev. B 79, 195321 (2009).
[4] C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005).
[5] J. Xia et al., Phys. Rev. Lett. 97, 167002 (2006).
[6] R. Roy, C. Kallin, Phys. Rev. B 77, 174513 (2008).
[7] R. Roy, arXiv:0803.2868 (2008).